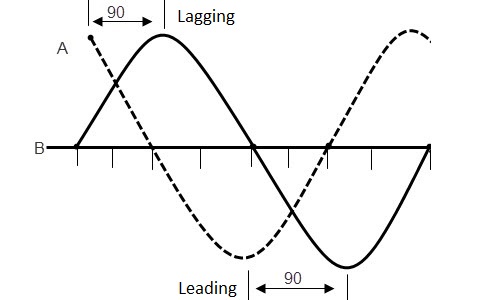
使用STM32测量两列信号的幅度比及相位差
STM32ADC同步采样
对于相位而言，我们采集的信号必须是同步的，否则讨论相位差毫无意义，而这也很容易理解：如果在采集过程就引入了时延，那计算所得的相位就包含了引入的时延。
这一部分主要讲解如何实现STM32ADC同步采样。
实现方式一
ADC 有一种同步模式，但配置较复杂，信号处理也不直接。已经有可用的教程，写得不错: 张十三的博客↗
实现方式二
下面介绍一种更加简单的方式：
只需要先开启两个ADC采样，然后开启定时器触发，这样定时器产生的触发信号同时到达两个ADC，两个ADC在接收到触发信号后，开始同步采样。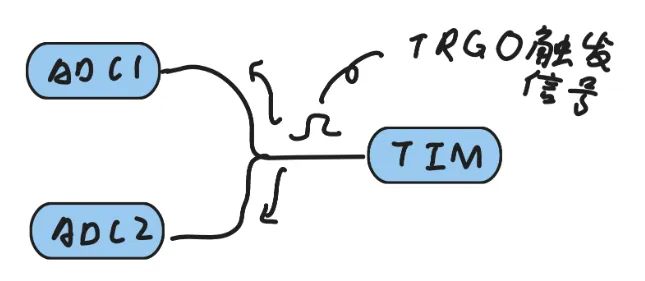 
工程配置：
ADC1配置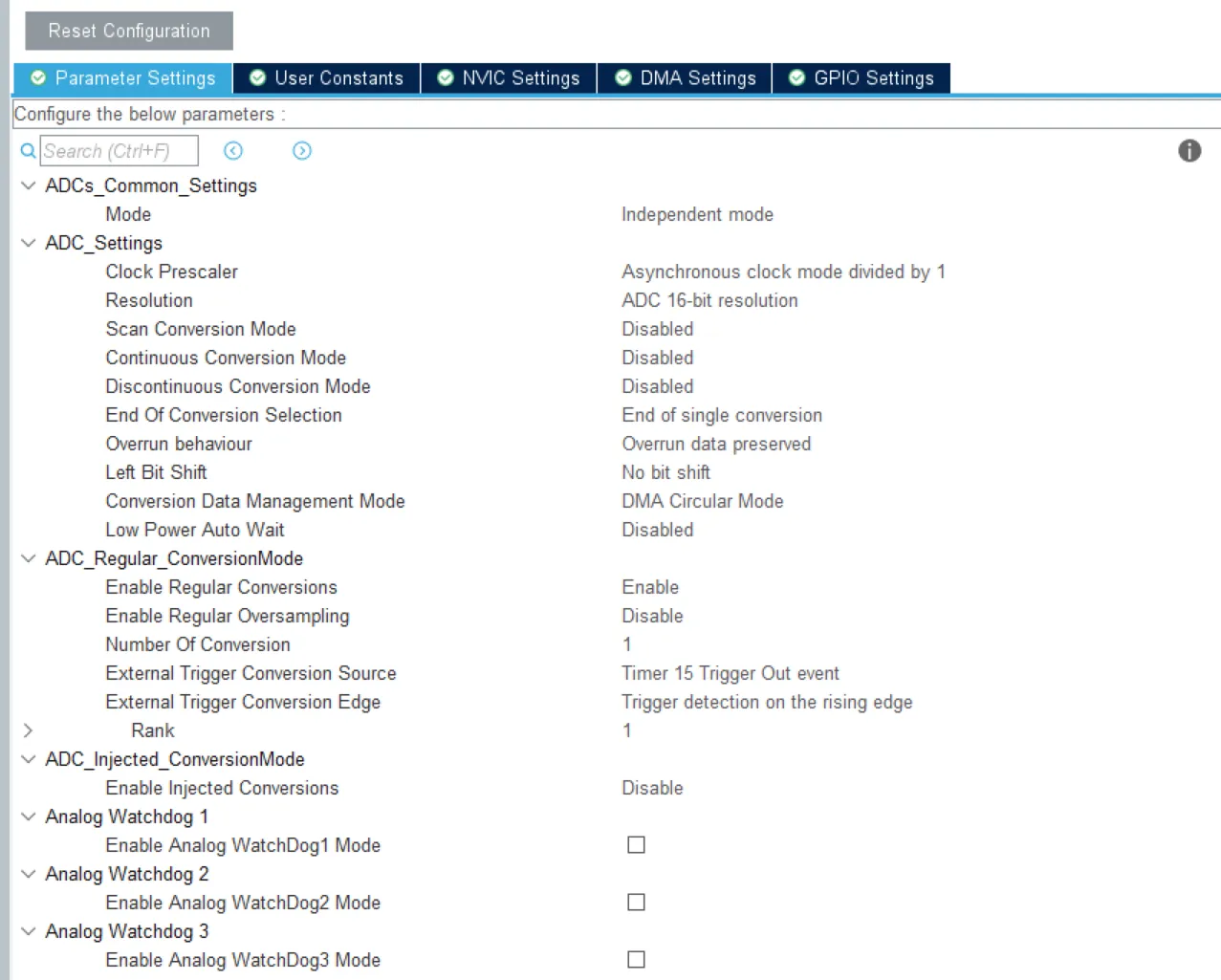 
ADC1DMA配置 
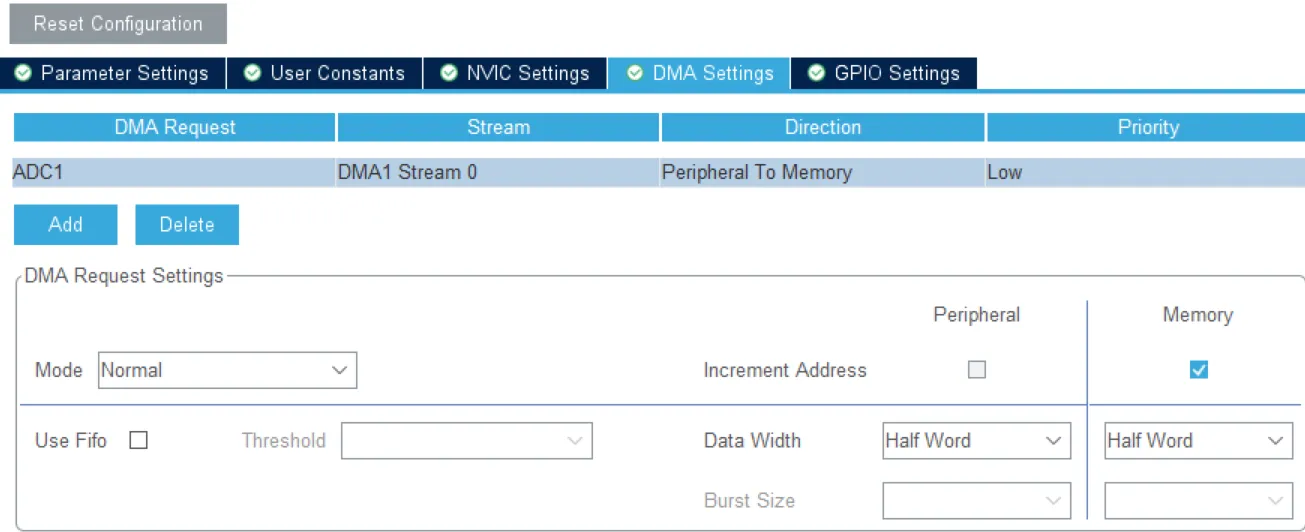ADC2配置及其DMA配置同ADC1
TIM15配置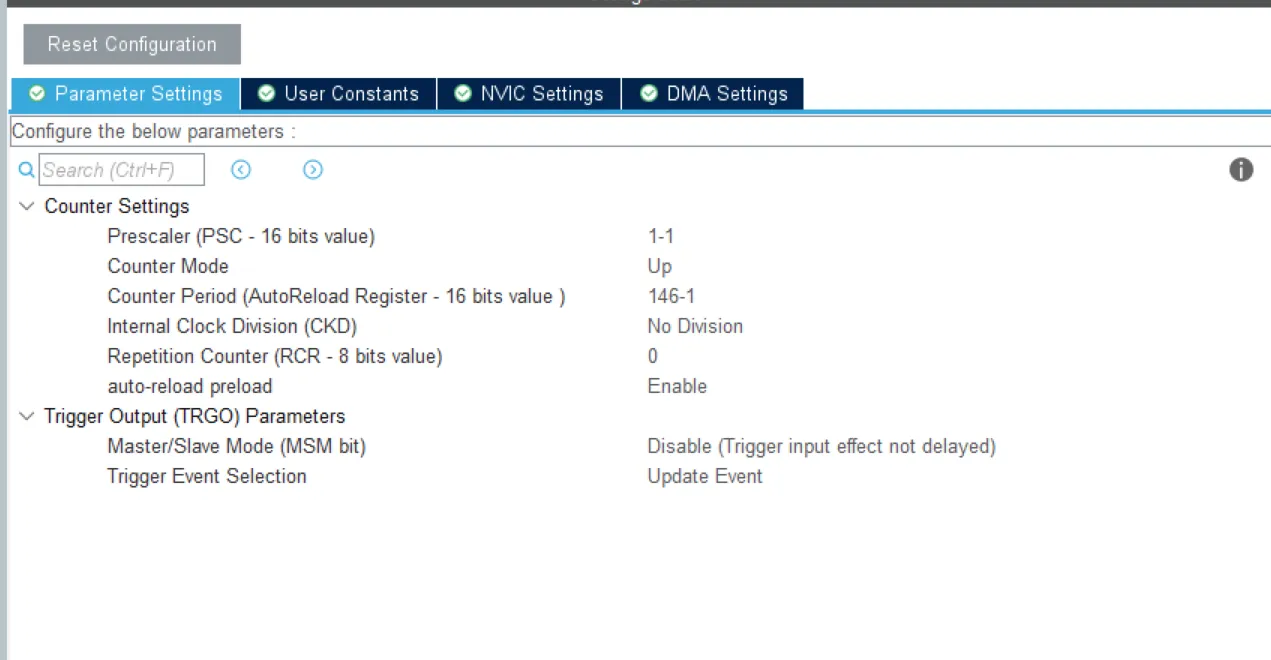 
TIM15决定ADC采样率，根据实际需要配置即可
代码展示：
建立ADC数组并分配RAM空间
ALIGN_32BYTES (uint16_t adc1_data[FFT_LENGTH]) __attribute__((section(".ARM.__at_0x30000000")));
ALIGN_32BYTES (uint16_t adc2_data[FFT_LENGTH]) __attribute__((section(".ARM.__at_0x30020000")));
__IO uint8_t AdcConvEnd = 0; //采集完成标志
ADC采集函数，调用即完成采样
void adc_init(void)
{
MX_ADC1_Init();
MX_ADC2_Init();
if (HAL_ADCEx_Calibration_Start(&hadc1, ADC_CALIB_OFFSET, ADC_SINGLE_ENDED) != HAL_OK)//鐢靛帇鏍″噯
{
//printf("hadc1 error with HAL_ADCEx_Calibration_Start\r\n");
Error_Handler();
}
if (HAL_ADC_Start_DMA(&hadc1, (uint32_t *)adc1_data, FFT_LENGTH) != HAL_OK)
{
//printf("hadc1 error with HAL_ADC_Start_DMA\r\n");
Error_Handler();
}
if (HAL_ADCEx_Calibration_Start(&hadc2, ADC_CALIB_OFFSET, ADC_SINGLE_ENDED) != HAL_OK)
{
//printf("hadc1 error with HAL_ADCEx_Calibration_Start\r\n");
Error_Handler();
}
if (HAL_ADC_Start_DMA(&hadc2, (uint32_t *)adc2_data, FFT_LENGTH) != HAL_OK)
{
//printf("hadc1 error with HAL_ADC_Start_DMA\r\n");
Error_Handler();
}
HAL_TIM_Base_Start(&htim15);
while (!AdcConvEnd);
AdcConvEnd = 0;
HAL_ADC_Stop_DMA(&hadc2);
HAL_ADC_Stop_DMA(&hadc1);
HAL_TIM_Base_Stop(&htim15);
}
中断回调函数
void HAL_ADC_ConvCpltCallback(ADC_HandleTypeDef* hadc)
{
AdcConvEnd = 1;
}
FFT计算幅值比及相位差
void FFT_Init1(float* fundamental_magnitude,float* fundamental_phase)
{
for(int i=0; i<FFT_LENGTH; i++)
{
q1[i].real = adc1_data[i] *3.3/65536;
q1[i].imag = 0;
}
FFT(q1, 13);
/* 计算幅度和相位 */
for(uint32_t i=0; i<FFT_LENGTH/2; i++)
{
// 计算模值
float real = q1[i].real;
float imag = q1[i].imag;
// 缓存中间结果，减少重复计算
float real_square = real * real;
float imag_square = imag * imag;
arm_sqrt_f32(real_square + imag_square, &magnitude11[i]);
phase11[i] = atan2f(imag, real);
}
/* 找出基频成分（幅度最大的非零频率） */
uint32_t fundamental_idx = 0;
float max_mag = 0;
for(uint32_t i=2; i<FFT_LENGTH/2; i++) // 跳过直流分量
{
if(magnitude11[i] > max_mag)
{
max_mag = magnitude11[i];
fundamental_idx = i;
}
}
/* 获取基频的幅度和相位 */
*fundamental_magnitude = magnitude11[fundamental_idx];
*fundamental_phase = phase11[fundamental_idx]; // 弧度
}
float FFT_Init2(float* fundamental_magnitude,float* fundamental_phase)
{
for(uint32_t i=0; i<FFT_LENGTH; i++)
{
q1[i].real = adc2_data[i] *3.3/65536;
q1[i].imag = 0;
}
FFT(q1, 13);
/* 计算幅度和相位 */
for(uint32_t i=0; i<FFT_LENGTH/2; i++)
{
// 计算模值
float real = q1[i].real;
float imag = q1[i].imag;
float real_square = real * real;
float imag_square = imag * imag;
arm_sqrt_f32(real * real + imag * imag, &magnitude22[i]);
phase22[i] = atan2f(imag, real);
}
/* 找出基频成分（幅度最大的非零频率） */
uint32_t fundamental_idx = 0;
float max_mag = 0;
for(uint32_t i=2; i<FFT_LENGTH/2; i++) // 跳过直流分量
{
if(magnitude22[i] > max_mag)
{
max_mag = magnitude22[i];
fundamental_idx = i;
}
}
/* 获取基频的幅度和相位 */
*fundamental_magnitude = magnitude22[fundamental_idx];
*fundamental_phase = phase22[fundamental_idx]; // 弧度
return 240000000.0*fundamental_idx/(FFT_LENGTH*146.0);//返回被测信号频率
}FFT算法参考之前的博客“更高性能的FFT/IFFT”
在上述代码中，有两点需要解释: 1、寻找基频,即找到该信号的特征频点
for(uint32_t i=2; i<FFT_LENGTH/2; i++) // 跳过直流分量
{
if(magnitude22[i] > max_mag)
{
max_mag = magnitude22[i];
fundamental_idx = i;
}
} 2、计算反正切
phase22[i] = atan2f(imag, real);FFT输出的每个频点都是复数（real + imag·j），可以表示为：
A·e^(jθ) = A·cosθ + j·A·sinθ其中：
•A是幅度（通过sqrt(real² + imag²)计算）
•θ是相位（通过atan2(imag,real)计算）
普通atan(y/x)存在缺陷：
•无法区分象限（例如-1/-1和1/1的结果相同）
•当x=0时会除零错误
atan2(y,x)能正确处理所有情况：
atan2(1,1) = π/4 // 第一象限
atan2(1,-1) = 3π/4 // 第二象限
atan2(-1,-1) = -3π/4 // 第三象限
atan2(-1,1) = -π/4 // 第四象限
atan2(1,0) = π/2 // y轴正方向总结
adc_init();
FFT_Init1(&mag1,&phase1);
FFT_Init2(&mag2,&phase2);
gain=mag2/mag1;
phase=phase2-phase1;gain即为幅度比， phase即为相位差。
Thanks for reading!